Biography
Yiming Meng is currently a Postdoctoral Research Associate in the Coordinated Science Laboratory at The Grainger College of Engineering, University of Illinois Urbana-Champaign (UIUC), working with Dr. Melkior Ornik. Before joining UIUC, he was a Postdoctoral Fellow at the Department of Applied Mathematics of the University of Waterloo (UWaterloo), where he worked with Dr. Jun Liu. He received his Ph.D. in Applied Mathematics from UWaterloo in October 2022, advised by Dr. Jun Liu and Dr. N.Sri.Namachchivaya.
His research addresses "intelligent" control synthesis for nonlinear dynamical systems operating in uncertain environments from a bottom-up perspective, with applications in diverse fields such as robotics, cyber-physical systems, mechanics, and other physical sciences.
Interests
- Stochastic hybrid dynamical systems and data-driven control
- Physics-informed machine learning for decision-making
- Multi-agent planning, dimension reduction, and optimal control
- Formal methods for control design
- Stochastic bifurcation
Education
-
Ph.D. in Applied Mathematics
University of Waterloo, Canada
-
M.Sc. in Process System Engineering
Imperial College London, UK
-
B.Eng. in Chemical Engineering
Tianjin Universiy, China
Academic Positions
Postdoctoral Research Associate
Coordinated Science Laboratory, University of Illinois Urbana-Champaign
Postdoctoral Fellow
Department of Applied Mathematics, University of Waterloo
Research Assistant
Sustainable Gas Institute, Imperial College London
Recent News
Research
*
For systems with limited knowledge, identifying system properties from observable data is vital to decision-making. We develop data-driven tools to estimate the system transition, winning set (with respect to the control objectives) and safe operation ranges, as well as to synthesize feasible controllers.
In continuous environments, optimality-related quantities for finite-dimensional dynamical systems usually exist in the lifted function/functional spaces, which are solutions to optimality-induced partial differential equations (PDEs). We develop analysis and computation tools in this regard.
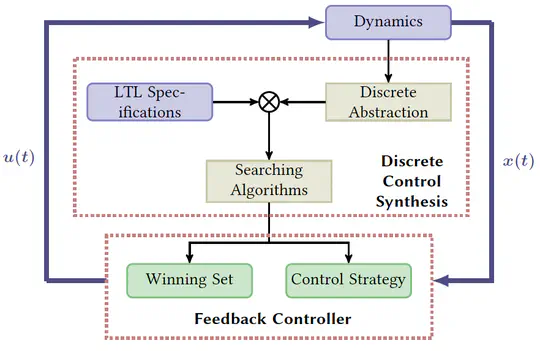
Formal abstractions enable autonomous decision-making of dynamical systems to achieve complex tasks and compute a holistic reference on controllable regions of initial conditions (winning sets) with quantifiable errors. We develop abstraction analysis and computation tools for stochastic formal verification and control synthesis.
As a crucial step before implementing controls for systems with uncertainties, it is necessary to gain a better understanding of the solution’s behaviors, such as the continuity/differentiability, stability, reachability, and safety-related properties. We develop fundamental mathematical analysis and novel analytical tools addressing safety-critical control.
Recent Publications
Quickly discover relevant content by filtering publications.
(2024).
Koopman-Based Learning of Infinitesimal Generators without Operator Logarithm.
In 2024 IEEE Conference on Decision and Control (CDC), to appear.
(2024).
Almost Sure Asymptotic Stability of Parabolic SPDEs with Small Multiplicative Noise.
Dynamical Systems.
(2024).
Data-driven optimal control of unknown nonlinear dynamical systems using the Koopman operator.
Submitted to 7th Annual Learning for Dynamics & Control Conference (L4DC), under review.
(2024).
Learning Koopman-based Stability Certificates for Unknown Nonlinear Systems.
Submitted to 7th Annual Learning for Dynamics & Control Conference (L4DC), under review.
(2024).
Resolvent-Type Data-Driven Learning of Generators for Unknown Continuous-Time Dynamical Systems.
Submitted to IEEE Transaction on Automatic Control, under review.
Contact
To learn more about my work, you can explore my Research page, where I’ve summarized some of my representative research outcomes. For scholars interested in my research areas and seeking collaboration, please feel free to get in touch with me if you would like to explore further opportunities.
- ymmeng@illinois.edu
- 1308 W Main St, Urbana, IL 61801